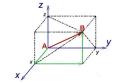
Найти угол между двумя. Угол между прямыми

Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x 1 ; y 1 ; z 1) и b = (x 2 ; y 2 ; z 2), то сможете найти угол. Точнее, косинус угла по формуле:

Посмотрим, как эта формула работает на конкретных примерах:

Задача. В кубе ABCDA 1 B 1 C 1 D 1 отмечены точки E и F - середины ребер A 1 B 1 и B 1 C 1 соответственно. Найдите угол между прямыми AE и BF.

Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA 1 соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.

Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E - середина отрезка A 1 B 1 , ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).

Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F - середина отрезка B 1 C 1 . Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак, направляющие векторы готовы. Косинус угла между прямыми - это косинус угла между направляющими векторами, поэтому имеем:

Задача. В правильной трехгранной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, отмечены точки D и E - середины ребер A 1 B 1 и B 1 C 1 соответственно. Найдите угол между прямыми AD и BE.

Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z - вдоль AA 1 . Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.

Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D - середина отрезка A 1 B 1 . Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).

Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E - серединой отрезка C 1 B 1 - чуть сложнее. Имеем:

Осталось найти косинус угла:

Задача. В правильной шестигранной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , все ребра которой равны 1, отмечены точки K и L - середины ребер A 1 B 1 и B 1 C 1 соответственно. Найдите угол между прямыми AK и BL.

Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y - через середины отрезков AB и DE, а ось z - вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:

Точки K и L - середины отрезков A 1 B 1 и B 1 C 1 соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:

Теперь найдем косинус угла:

Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F - середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.

Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.

Точки E и F - середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек:
A = (0; 0; 0); B = (1; 0; 0)

Зная точки, найдем координаты направляющих векторов AE и BF:

Координаты вектора AE совпадают с координатами точки E, поскольку точка A - начало координат. Осталось найти косинус угла:

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l 1 параллельна l 2 тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Угол между прямой и плоскостью

Пусть прямая d - не перпендикулярна плоскости θ;
d ′− проекция прямой d на плоскость θ;
Наименьший из углов между прямыми d и d ′ мы назовем углом между прямой и плоскостью .
Обозначим его как φ=(d ,θ)
Если d ⊥θ , то (d ,θ)=π/2

Oi →j →k →− прямоугольная система координат.
Уравнение плоскости:

θ:Ax +By +Cz +D =0

Считаем, что прямая задана точкой и направляющим вектором: d [M 0,p →]
Вектор n →(A ,B ,C )⊥θ
Тогда остается выяснить угол между векторами n → и p →, обозначим его как γ=(n →,p →).

Если угол γ<π/2 , то искомый угол φ=π/2−γ .

Если угол γ>π/2 , то искомый угол φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Тогда, угол между прямой и плоскостью можно считать по формуле:

sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23

Вопрос29. Понятие квадратичной формы. Знакоопределенность квадратичных форм.

Квадратичной формой j (х 1 , х 2 , …, x n) n действительных переменных х 1 , х 2 , …, x n называется сумма вида
, (1)

где a ij – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что a ij = a ji .

Квадратичная форма называется действительной, если a ij Î ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица
Т. е. А Т = А . Следовательно, квадратичная форма (1) может быть записана в матричном виде j (х ) = х Т Ах , где х Т = (х 1 х 2 … x n ). (2)

И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А . (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.

положительно определенной (или строго положительной), если

j (х ) > 0 , для любого х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).

Матрица А положительно определенной квадратичной формы j (х ) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.

Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если

j (х ) < 0, для любого х = (х 1 , х 2 , …, x n ), кроме х = (0, 0, …, 0).

Аналогично как и выше, матрица отрицательно определенной квад-ратичной формы также называется отрицательно определенной.

Следовательно, положительно (отрицательно) определенная квадра-тичная форма j (х ) достигает минимального (максимального) значения j (х* ) = 0 при х* = (0, 0, …, 0).

Отметим, что большая часть квадратичных форм не является знакоопределенными, то есть они не являются ни положительными, ни отрицательными. Такие квадратичные формы обращаются в 0 не только в начале системы координат, но и в других точках.

Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.

Главными минорами квадратичной формы называются миноры:

то есть это миноры порядка 1, 2, …, n матрицы А , расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А .

Критерий положительной определенности (критерий Сильвестра)

х ) = х Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть: М 1 > 0, M 2 > 0, …, M n > 0. Критерий отрицательной определенности Для того чтобы квадратичная форма j (х ) = х Т Ах была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, т. е.: М 1 < 0, M 2 > 0, М 3 < 0, …, (–1) n

Угол φ общими уравнениями A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0, вычисляется по формуле:

Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x 1)/m 1 = (y-y 1)/n 1 и (x-x 2)/m 2 = (y-y 2)/n 2 , вычисляется по формуле:

Расстояние от точки до прямой

Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости

Частные случаи .

o Если в уравнении (8) , то плоскость проходит через начало координат.

o При (,) плоскость параллельна оси(оси, оси) соответственно.

o При (,) плоскость параллельна плоскости(плоскости, плоскости).

Решение: используем (7)

Ответ: общее уравнение плоскости .

Пример.

Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости . Запишите координаты всех нормальных векторов этой плоскости.

Нам известно, что коэффициенты при переменных x, y и z в общем уравнении плоскости являются соответствующими координатами нормального вектора этой плоскости. Следовательно, нормальный вектор заданной плоскостиимеет координаты. Множество всех нормальных векторов можно задать как.

Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку , а- нормальный вектор этой плоскости.

Приведем два решения этой задачи.

Из условия имеем . Подставляем эти данные в общее уравнение плоскости, проходящей через точку:

Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку .

Плоскость, которая параллельна координатной плоскости Oyz, может быть задана общим неполным уравнением плоскости вида . Так как точкапринадлежит плоскости по условию, то координаты этой точки должны удовлетворять уравнению плоскости, то есть, должно быть справедливо равенство. Отсюда находим. Таким образом, искомое уравнение имеет вид.

Решение. Векторное произведение по определению 10.26 ортогонально векторам p и q. Следовательно, оно ортогонально искомой плоскости и вектор можно взять в качестве ее нормального вектора. Найдем координаты вектора n:

то есть . Используя формулу (11.1), получим

Раскрыв в этом уравнении скобки, приходим к окончательному ответу.

Ответ: .

Перепишем вектор нормали в виде и найдём его длину:

Согласно вышесказанному:

Ответ :

У параллельных плоскостей один и тот же вектор нормали. 1) Из уравнения найдём вектор нормали плоскости:.

2) Уравнение плоскости составим по точкеи вектору нормали:

Ответ :

Векторное уравнение плоскости в пространстве

Параметрическое уравнение плоскости в пространстве

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:

Составить уравнение плоскости, проходящей через данную точку M (x 0, y 0, z 0) перпендикулярно данному вектору n = {A , B , C } .

Решение. Пусть P (x , y , z ) - произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор MP = {x − x 0, y − y 0, z − z 0} ортогонален вектору n = {A , B , C } (рис.1).

Написав условие ортогональности этих векторов (n, MP ) = 0 в координатной форме, получим:

Уравнение плоскости по трем точкам

В векторном виде

В координатах

Взаимное расположение плоскостей в пространстве

– общие уравнения двух плоскостей. Тогда:

1) если , то плоскости совпадают;

2) если , то плоскости параллельны;

3) если или , то плоскости пересекаются и системауравнений

(6)

является уравнениями прямой пересечения данных плоскостей.

Составить параметрические уравнения следующих прямых:

Решение : Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений снимаем точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

Таким образом: б) Рассмотрим канонические уравнения . Выбор точки здесь несложен, но коварен: (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор , а на оставшееся место поставим ноль: .

Составим параметрические уравнения прямой:

в) Перепишем уравнения в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули : . На оставшееся место ставим единицу : . Вместо единицы подойдёт любое число, кроме нуля.

Запишем параметрические уравнения прямой:

а. Пусть даны две прямые Эти прямые как было указано в главе 1, образуют различные положительные и отрицательные углы, которые при этом могут быть как острыми, так и тупыми. Зная один из этих углов мы легко найдем какой-либо другой.

Между прочим, у всех этих углов численная величина тангенса одна и та же, различие может быть только в знаке

Уравнения прямых. Числа суть проекции направляющих векторов первой и второй прямой Угол между этими векторами равен одному из углов, образуемых прямыми линиями. Поэтому задача сводится к определению угла между векторами, Мы получим

Для простоты можно условиться под углом между двумя прямыми понимать острый положительный угол (как, например, на рис. 53).

Тогда тангенс этого угла будет всегда положительным. Таким образом, если в правой части формулы (1) получится знак минус, то мы его должны отбросить, т. е. сохранить только абсолютную величину.

Пример. Определить угол между прямыми

По формуле (1) имеем

с. Если будет указано, какая из сторон угла является его началом и какая концом, то, отсчитывая всегда направление угла против часовой стрелки, мы можем формулы (1) извлечь нечто большее. Как нетрудно убедиться из рис. 53 знак получающийся в правой части формулы (1), будет указывать, какой именно - острый или тупой - угол образует вторая прямая с первой.

(Действительно, из рис, 53 мы усматриваем, что угол между первым и вторым направляющими векторами или равен искомому углу между прямыми, или отличается от него на ±180°.)

d. Если прямые параллельны, то параллельны и их направляющие векторы, Применяя условие параллельности двух векторов получим!

Это есть условием необходимое и достаточное для параллельности двух прямых.

Пример. Прямые

параллельны, так как

e. Если прямые перпендикулярны то их направляющие векторы тоже перпендикулярны. Применяя условие перпендикулярности двух векторов мы получим условие перпендикулярности двух прямых а именно

Пример. Прямые

перпендикулярны ввиду того, что

В связи с условиями параллельности и перпендикулярности решим следующие две задачи.

f. Через точку провести прямую параллельно данной прямой

Решение проводится так. Так как искомая прямая параллельна данной, то за ее направляющий вектор можно взять тот же самый, что и у данной прямой, т. е. вектор с проекциями А и В. А тогда уравнение искомой прямой напишется в форме (§ 1)

Пример. Уравнение прямой, проходящей через точку (1; 3) параллельно прямой

будет следующее!

g. Через точку провести прямую перпендикулярно данной прямой

Здесь за направляющий вектор уже не годится брать вектор с проекциями А и , а надо веять вектор, ему перпендикулярный. Проекции этого вектора должны быть выбраны следовательно, согласно условию перпендикулярности обоих векторов, т. е. согласно условию

Выполнить же это условие можно бесчисленным множеством способов, так как здесь одно уравнение с двумя неизвестными Но проще всего взять иди же Тогда уравнение искомой прямой напишется в форме

Пример. Уравнение прямой, проходящей через точку (-7; 2) в перпендикулярной прямой

будет следующее (по второй формуле)!

h. В том случаем когда прямые заданы уравнениями вида

переписывая эти уравнения иначе, имеем

Задача 1

Найти косинус угла между прямыми $\frac{x+3}{5} =\frac{y-2}{-3} =\frac{z-1}{4} $ и $\left\{\begin{array}{c} {x=2\cdot t-3} \\ {y=-t+1} \\ {z=3\cdot t+5} \end{array}\right. $.

Пусть в пространстве заданы две прямые: $\frac{x-x_{1} }{m_{1} } =\frac{y-y_{1} }{n_{1} } =\frac{z-z_{1} }{p_{1} } $ и $\frac{x-x_{2} }{m_{2} } =\frac{y-y_{2} }{n_{2} } =\frac{z-z_{2} }{p_{2} } $. Выберем в пространстве произвольную точку и проведем через неё две вспомогательные прямые, параллельные данным. Углом между данными прямыми является любой из двух смежных углов, образованных вспомогательными прямыми. Косинус одного из углов между прямыми можно найти по известной формуле $\cos \phi =\frac{m_{1} \cdot m_{2} +n_{1} \cdot n_{2} +p_{1} \cdot p_{2} }{\sqrt{m_{1}^{2} +n_{1}^{2} +p_{1}^{2} } \cdot \sqrt{m_{2}^{2} +n_{2}^{2} +p_{2}^{2} } } $. Если значение $\cos \phi >0$, то получен острый угол между прямыми, если $\cos \phi

Канонические уравнения первой прямой: $\frac{x+3}{5} =\frac{y-2}{-3} =\frac{z-1}{4} $.

Канонические уравнения второй прямой можно получить из параметрических:

\ \ \

Таким образом, канонические уравнения данной прямой: $\frac{x+3}{2} =\frac{y-1}{-1} =\frac{z-5}{3} $.

Вычисляем:

\[\cos \phi =\frac{5\cdot 2+\left(-3\right)\cdot \left(-1\right)+4\cdot 3}{\sqrt{5^{2} +\left(-3\right)^{2} +4^{2} } \cdot \sqrt{2^{2} +\left(-1\right)^{2} +3^{2} } } =\frac{25}{\sqrt{50} \cdot \sqrt{14} } \approx 0,9449.\]

Задача 2

Первая прямая проходит через заданные точки $A\left(2,-4,-1\right)$ и $B\left(-3,5,6\right)$, вторая прямая -- через заданные точки $C\left(1,-2,8\right)$ и $D\left(6,7,-2\right)$. Найти расстояние между этими прямыми.

Пусть некоторая прямая перпендикулярна к прямым $AB$ и $CD$ и пересекает их в точках $M$ и $N$ соответственно. При таких условиях длина отрезка $MN$ равна расстоянию между прямыми $AB$ и $CD$.

Строим вектор $\overline{AB}$:

\[\overline{AB}=\left(-3-2\right)\cdot \bar{i}+\left(5-\left(-4\right)\right)\cdot \bar{j}+\left(6-\left(-1\right)\right)\cdot \bar{k}=-5\cdot \bar{i}+9\cdot \bar{j}+7\cdot \bar{k}.\]

Пусть отрезок, изображающий расстояние между прямыми, проходит через точку $M\left(x_{M} ,y_{M} ,z_{M} \right)$ на прямой $AB$.

Строим вектор $\overline{AM}$:

\[\overline{AM}=\left(x_{M} -2\right)\cdot \bar{i}+\left(y_{M} -\left(-4\right)\right)\cdot \bar{j}+\left(z_{M} -\left(-1\right)\right)\cdot \bar{k}=\] \[=\left(x_{M} -2\right)\cdot \bar{i}+\left(y_{M} +4\right)\cdot \bar{j}+\left(z_{M} +1\right)\cdot \bar{k}.\]

Векторы $\overline{AB}$ и $\overline{AM}$ совпадают, следовательно, они коллинеарны.

Известно, что если векторы $\overline{a}=x_{1} \cdot \overline{i}+y_{1} \cdot \overline{j}+z_{1} \cdot \overline{k}$ и $\overline{b}=x_{2} \cdot \overline{i}+y_{2} \cdot \overline{j}+z_{2} \cdot \overline{k}$ коллинеарны, то их координаты пропорциональны, то есть $\frac{x_{{\it 2}} }{{\it x}_{{\it 1}} } =\frac{y_{{\it 2}} }{{\it y}_{{\it 1}} } =\frac{z_{{\it 2}} }{{\it z}_{{\it 1}} } $.

$\frac{x_{M} -2}{-5} =\frac{y_{M} +4}{9} =\frac{z_{M} +1}{7} =m$, где $m$ -- результат деления.

Отсюда получаем: $x_{M} -2=-5\cdot m$; $y_{M} +4=9\cdot m$; $z_{M} +1=7\cdot m$.

Окончательно получаем выражения для координат точки $M$:

Строим вектор $\overline{CD}$:

\[\overline{CD}=\left(6-1\right)\cdot \bar{i}+\left(7-\left(-2\right)\right)\cdot \bar{j}+\left(-2-8\right)\cdot \bar{k}=5\cdot \bar{i}+9\cdot \bar{j}-10\cdot \bar{k}.\]

Пусть отрезок, изображающий расстояние между прямыми, проходит через точку $N\left(x_{N} ,y_{N} ,z_{N} \right)$ на прямой $CD$.

Строим вектор $\overline{CN}$:

\[\overline{CN}=\left(x_{N} -1\right)\cdot \bar{i}+\left(y_{N} -\left(-2\right)\right)\cdot \bar{j}+\left(z_{N} -8\right)\cdot \bar{k}=\] \[=\left(x_{N} -1\right)\cdot \bar{i}+\left(y_{N} +2\right)\cdot \bar{j}+\left(z_{N} -8\right)\cdot \bar{k}.\]

Векторы $\overline{CD}$ и $\overline{CN}$ совпадають, следовательно, они коллинеарны. Применяем условие коллинеарности векторов :

$\frac{x_{N} -1}{5} =\frac{y_{N} +2}{9} =\frac{z_{N} -8}{-10} =n$, где $n$ -- результат деления.

Отсюда получаем: $x_{N} -1=5\cdot n$; $y_{N} +2=9\cdot n$; $z_{N} -8=-10\cdot n$.

Окончательно получаем выражения для координат точки $N$:

Строим вектор $\overline{MN}$:

\[\overline{MN}=\left(x_{N} -x_{M} \right)\cdot \bar{i}+\left(y_{N} -y_{M} \right)\cdot \bar{j}+\left(z_{N} -z_{M} \right)\cdot \bar{k}.\]

Подставляем выражения для координат точек $M$ и $N$:

\[\overline{MN}=\left(1+5\cdot n-\left(2-5\cdot m\right)\right)\cdot \bar{i}+\] \[+\left(-2+9\cdot n-\left(-4+9\cdot m\right)\right)\cdot \bar{j}+\left(8-10\cdot n-\left(-1+7\cdot m\right)\right)\cdot \bar{k}.\]

Выполнив действия, получаем:

\[\overline{MN}=\left(-1+5\cdot n+5\cdot m\right)\cdot \bar{i}+\left(2+9\cdot n-9\cdot m\right)\cdot \bar{j}+\left(9-10\cdot n-7\cdot m\right)\cdot \bar{k}.\]

Поскольку прямые $AB$ и $MN$ перпендикулярны, то скалярное произведение соответствующих векторов равно нулю, то есть $\overline{AB}\cdot \overline{MN}=0$:

\[-5\cdot \left(-1+5\cdot n+5\cdot m\right)+9\cdot \left(2+9\cdot n-9\cdot m\right)+7\cdot \left(9-10\cdot n-7\cdot m\right)=0;\] \

Выполнив действия, получаем первое уравнение для определения $m$ и $n$: $155\cdot m+14\cdot n=86$.

Поскольку прямые $CD$ и $MN$ перпендикулярны, то скалярное произведение соответствующих векторов равно нулю, то есть $\overline{CD}\cdot \overline{MN}=0$:

\ \[-5+25\cdot n+25\cdot m+18+81\cdot n-81\cdot m-90+100\cdot n+70\cdot m=0.\]

Выполнив действия, получаем второе уравнение для определения $m$ и $n$: $14\cdot m+206\cdot n=77$.

Находим $m$ и $n$, решив систему уравнений $\left\{\begin{array}{c} {155\cdot m+14\cdot n=86} \\ {14\cdot m+206\cdot n=77} \end{array}\right. $.

Применяем метод Крамера:

\[\Delta =\left|\begin{array}{cc} {155} & {14} \\ {14} & {206} \end{array}\right|=31734; \] \[\Delta _{m} =\left|\begin{array}{cc} {86} & {14} \\ {77} & {206} \end{array}\right|=16638; \] \[\Delta _{n} =\left|\begin{array}{cc} {155} & {86} \\ {14} & {77} \end{array}\right|=10731;\] \

Находим координаты точек $M$ и $N$:

\ \

Окончательно:

Окончательно записываем вектор $\overline{MN}$:

$\overline{MN}=\left(2,691-\left(-0,6215\right)\right)\cdot \bar{i}+\left(1,0438-0,7187\right)\cdot \bar{j}+\left(4,618-2,6701\right)\cdot \bar{k}$ или $\overline{MN}=3,3125\cdot \bar{i}+0,3251\cdot \bar{j}+1,9479\cdot \bar{k}$.

Расстояние между прямыми $AB$ и $CD$ -- это длина вектора $\overline{MN}$:$d=\sqrt{3,3125^{2} +0,3251^{2} +1,9479^{2} } \approx 3,8565$ лин. ед.